1、抛物线的参数方程可以是{x,x^2},为了把作图范围控制在有限区间内,需要进行变量替换:
{Tan[t],Tan[t]^2}
浸入三维空间,再沿着z轴上下平移,就得到抛物柱面:
{Tan[t],Tan[t]^2,0}+{0,0,Tan[v]}

2、抛物柱面是一个无限伸展的曲面,可以通过聚合变换,使之局限于单位球内部:

3、抛物线在平移的同时,采用余弦压缩,得到一个抛物线罩子:
{Cos[v] Tan[t], Cos[v] Tan[t]^2, Sin[v]}

4、抛物线罩子也是无限伸展的,采用聚合变换:
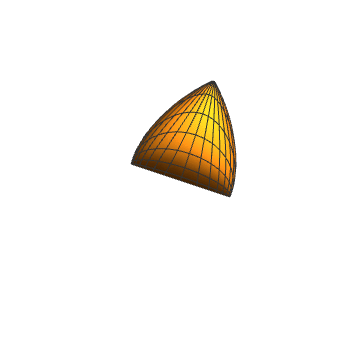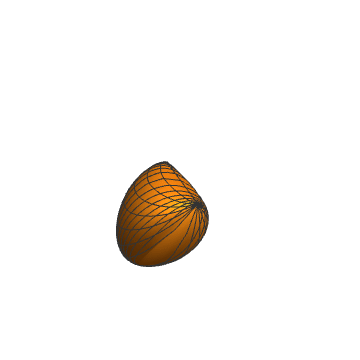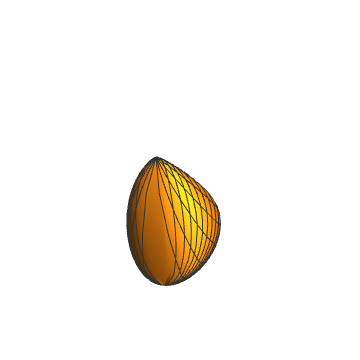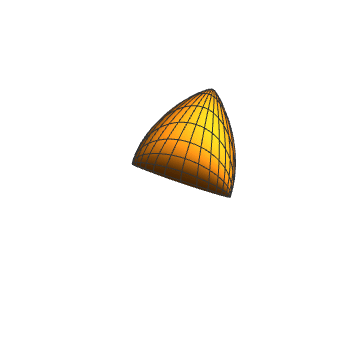
5、{Cos[2 v] Tan[t], Cos[2 v] Tan[t]^2, Cos[2 v] Tan[v]}:

6、上图的聚合:
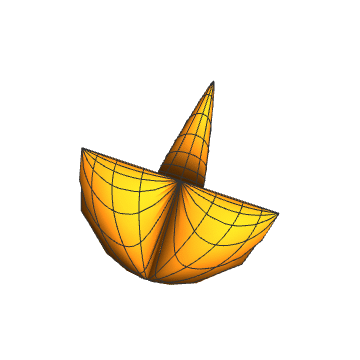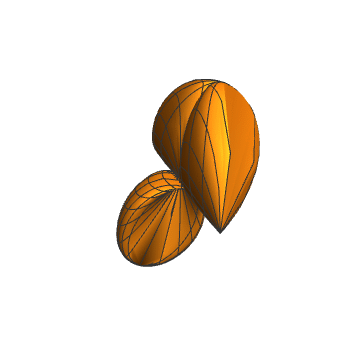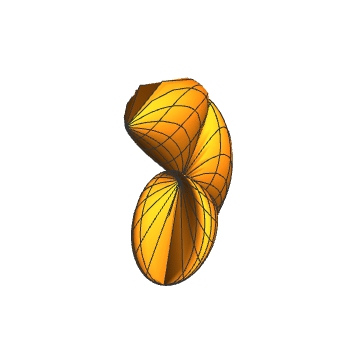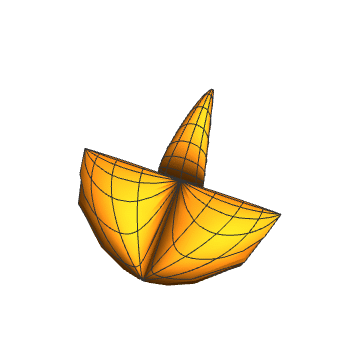
7、{Abs[Cos[2 v]] Tan[t], Abs[Cos[2 v]] Tan[t]^2, Abs[Cos[2 v]] Tan[v]}:

8、上图的聚合:
