1、y1=x^2与y2=√x在直角坐标系的图像如下:

2、联立曲线方程y1=x^2与y2=√x,求出二者的交点:
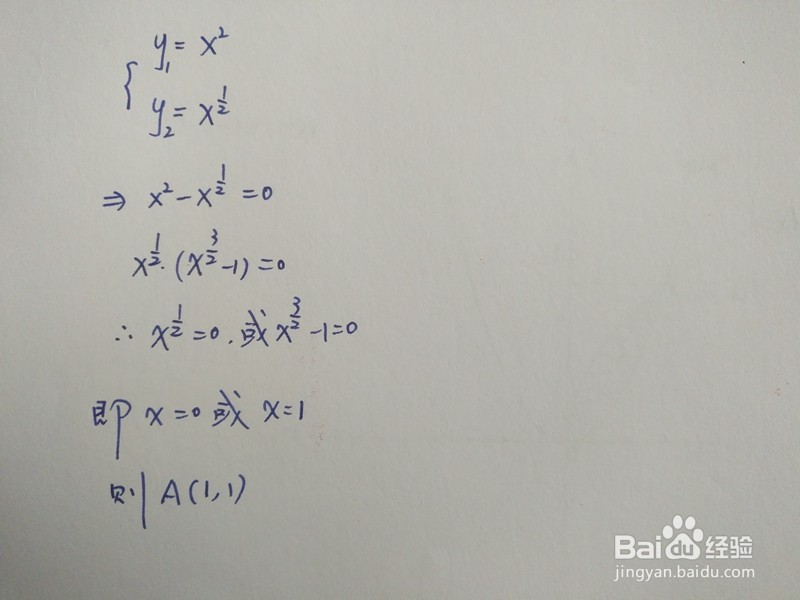
3、根据定积分面积公式,求出此时曲线围成的面积,主要步骤如下:
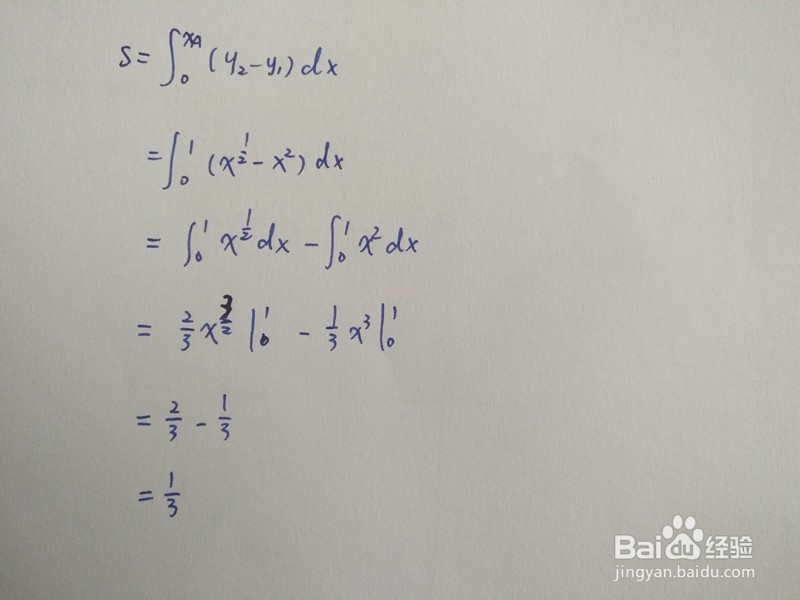
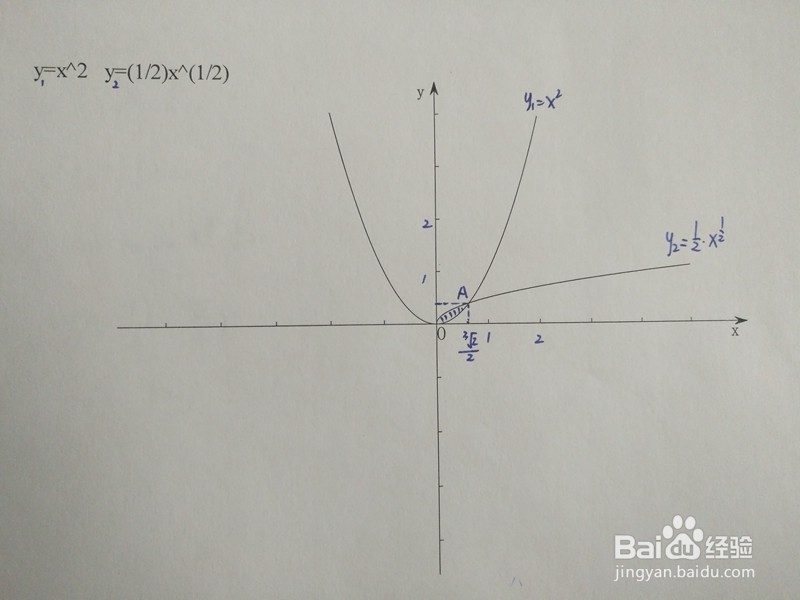
1、y1=x^2与y2=(1/2)√x在直角坐标系的图像如下:
2、联立曲线方程y1=x^2与y2=(1/2)√x,求出二者的交点:

3、根据定积分面积公式,求出此时曲线围成的面积,主要步骤如下:

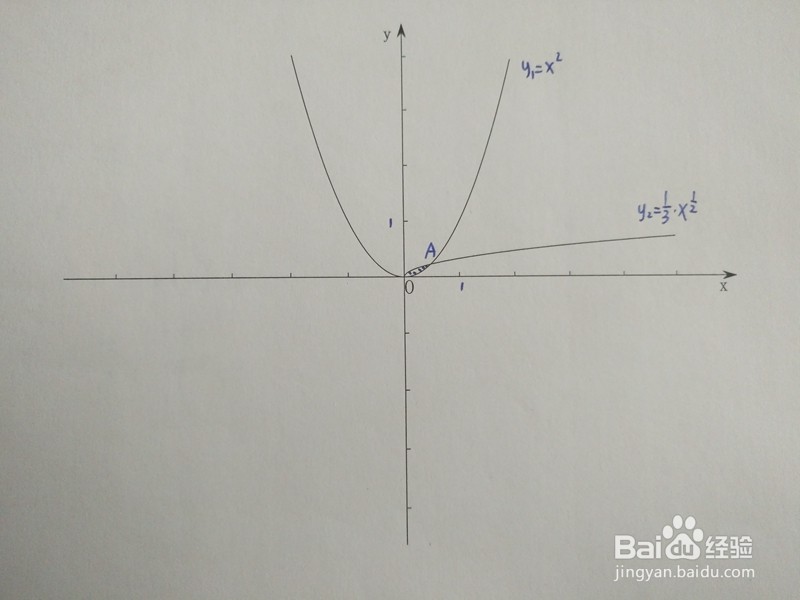
1、y1=x^2与y2=(1/3)√x在直角坐标系的图像如下:
2、联立曲线方程y1=x^2与y2=(1/3)√x,求出二者的交点:

3、根据定积分面积公式,求出此时曲线围成的面积,主要步骤如下:
